En los últimos años, las investigaciones en didáctica de las matemáticas han dado un giro importante hacia enfoques de corte histórico-cultural, basados en los aportes de la Teoría de la Actividad. De esta manera, la comprensión de los fenómenos asociados a la actividad de enseñanza (del lado del maestro), y de la actividad de aprendizaje (del lado del estudiante), debe necesariamente incluir en la explicación, los instrumentos semióticos de orden cultural que sirvieron de base para configurar las acciones de los sujetos inmersos en el acto educativo.
Esto lleva a una mirada diferente de lo que el estudiante hace en el aula de clase al resolver una tarea, pues ya no se trata simplemente de decir si el procedimiento es o no correcto, de acuerdo a un tipo de conocimiento considerado como válido: el conocimiento formal de las matemáticas. Se debe interpretar lo realizado en el marco de las condiciones culturales que delimitaron el accionar del sujeto, y por esta vía, comprender que lo realizado es correcto desde el punto de vista de la lógica de la acción que configura la actividad del estudiante (así no lo sea desde el punto de vista del conocimiento formalizado).
Esto permite hablar en términos de lo que el estudiante sabe hacer y no desde la deficiencia, desde lo que aún no sabe hacer, entregando nuevas herramientas al profesor para la toma de decisiones sobre como orientar el proceso de aprendizaje de los estudiantes. Así pues, en este artículo, analizamos algunos elementos de la Teoría de la Actividad, que nos permite constituir un marco específico para comprender la actividad matemática en el aula de clase y con base en estos elementos, analizamos la actividad de los estudiantes en una tarea específica para mostrar como la lógica de la acción de lo actuado por ellos nos enseña lo que saben hacer, generando así una mirada en positivo de la actividad matemática de los estudiantes.
“Asumimos la noción de actividad como una categoría filosófica que nos permite comprender la relación del sujeto humano, como ser social, [con] la realidad externa, relación mediatizada por el proceso de transformación y cambio de esta realidad” (Davidov, 1988, p. 11) 1. Así, la actividad es el conjunto de acciones humanas (organizadas y estructuradas), socialmente orientadas a un fin (intencional) (Leontiev, 1978; Ricoeur, 2001) 2 y regulada por la adscripción del sujeto a un sistema de prácticas en un campo de experiencias determinado (Obando 2015) 3. Sin embargo, dado que el individuo reflexiona sobre su práctica, se posiciona frente al sistema de prácticas que direcciona su accionar en el mundo, él re-significa su práctica, la transforma, constituyendo lo que podemos llamar su subjetividad: “La subjetividad aparece como forma de participación y contribución a la práctica social, de cambio y de avance, y así, como la forma en que las realizaciones prácticas de los humanos son conducidas hacia sí mismos, hacia otras personas, hacia su mundo” (Stetsenko, 2005, p. 82) 4. Pertenecen al dominio de la subjetividad los ideales, conductas y valores a los que apela el sujeto para darle sentido a su propia práctica.
La subjetivación es entonces el proceso por medio del cual el individuo se constituye como ser en función de su acción reflexiva y su posicionamiento frente al mundo. A partir de la subjetivación el individuo participa en los entornos de la actividad práctica, y, por ende, habita las instituciones, las hace vivir en la revisión y transformación continua de dichos sistemas de prácticas (Obando 2015, p. 50) 3.
En el marco antes expuesto, entendemos institución como:
un espacio simbólico (con límites más o menos definidos) de prácticas compartidas por un colectivo de individuos, los practicantes en esa comunidad, espacio donde se comparte, se negocia, se actúa con los otros (y donde también se excluye), en donde resuenan las voces presentes de muchos otros y las voces pasadas que han constituido la memoria cultural de la comunidad. Lo institucional es entonces todo ese sistema, o superestructura simbólica, que permite que el individuo sea un ser en y desde la cultura a través de su acción en y con otros. (Obando 2015, p. 51) 3.
En un marco institucional determinado, la práctica matemática de un sujeto, o grupo de sujetos tiene las marcas propias de un momento, época y lugar, comparte unas formas específicas de sensibilidad, de acción, maneras propias de ver y actuar. “Lo institucional genera sistemas de prácticas que disponen al individuo en un conjunto de formas de acción socialmente constituidas” (Obando, p. 51) 3. En el marco de lo institucional, el individuo es, se constituye, en tanto es reconocido por otros, en oposición a los otros (lo comunal se constituye sobre la base de las subjetividades de los individuos), en la medida que se inscribe en ese conjunto de prácticas socialmente compartidas: esta participación en las prácticas socialmente constituidas es el aprendizaje (Radford 2008, 2010) 5.
Aprender es un proceso reflexivo de transformación de las prácticas matemáticas que lo lleva a hacerse críticamente consciente de una forma codificada de pensar y de hacer (Radford, 2013) 6. La participación, no es imitación ni copia irreflexiva de los patrones de prácticas ya establecidas. Es la actividad del sujeto que reflexiona en y sobre los patrones de actividad culturalmente constituidos (Radford, 2006) 7 en el marco de su sistema de actividades prácticas institucionalizadas.
Referiremos como “sistema de prácticas” a ese conjunto o matriz de condiciones sociales e individuales que hacen posible en los individuos la orientación objetiva de la acción y el posicionamiento frente a ella (noción de práctica en el sentido de Bourdieu), y como “práctica actuada”, “actividad práctica” o simplemente “práctica” a la actividad humana particular, que se da dentro de, a partir de, esa matriz determinada por un sistema de prácticas, y no a la matriz en sí misma. (Obando, 2015, p. 53) 3
Práctica matemática
Al decir “práctica matemática” se quiere referir al conjunto de acciones de los individuos (en sus relaciones entre sí, y con el medio) que, en el curso de su actividad (sobre diversos tipos de eventos o fenómenos), orientan sus procesos de objetivación y subjetivación tanto de la cantidad y la forma (por ejemplo, medir, contar, comprar, vender, intercambiar, construir, fabricar, estimar, describir, localizar, etc.), como de la variación de una u otra (movimiento, cambio, comparación, transformación, etc.). (Obando, 2015, p. 55) 3.
En la anterior aproximación a la noción de práctica matemática, se debe entender que las acciones son mediadas culturalmente a partir de los recursos disponibles para la acción: los instrumentos, las técnicas, los discursos, los conceptos, los objetos de conocimiento y los problemas. Así, para caracterizar una práctica matemática, se debe prestar atención a:
- los objetos de conocimiento con, y sobre los cuales se actúa: “construcciones simbólicas (constituidas históricamente), solo accesibles a través del signo (ecuaciones, gráficas, gestos, etc.), de los procedimientos configurados sobre tales signos (construcciones, algoritmos, etc.) y de los conceptos elaborados en relación con signos e instrumentos (definiciones, proposiciones, enunciados, etc.)”. (Obando, 2015, p. 60) 3
- los conceptos que se enuncian sobre tales objetos.
- los instrumentos para la acción: “conjunto de recursos simbólicos (signos, símbolos, textos, fórmulas, medios gráfico-simbólicos, artefactos, software, gestos, etc.) que constituyen los medios para la acción matemática”. (Obando, 2015, p. 59) 3
- los procedimientos que permiten tales instrumentos. Formas específicas de acción, configurados en función de los instrumentos disponibles, y de los problemas por resolver.
- los problemas que orientan objetivamente la acción de los individuos, los “campos válidos de indagación y de cuyo tratamiento emerge el conocimiento matemático objeto de estudio”. (Obando, 2015, p. 57) 3
- las formas de discursividad que permiten poner el hacer en el lenguaje (formas de decir, de escribir, de comunicar). El lenguaje como vehículo para realizar las operaciones matemáticas, pero también como el medio para expresarlas. (Obando, 2015, p. 59) 3
Un ejemplo de análisis de la práctica matemática de estudiantes de grado 3
La siguiente tarea, al igual que las imágenes de referencia y comentarios mostrados en este ejemplo son tomadas casi textualmente de Obando (2015) 3, páginas 167 a 170.
La tarea:
| NÚMERO DE DULCES | PRECIO |
|---|---|
| 2 | |
| 3 | |
| 4 | |
| 6 | |
| 8 | $120 |
| 10 |
Andrés pagó $120 por 8 dulces iguales. ¿Cuánto pagará por tres dulces? Respuesta:
Ahora teniendo en cuenta los datos del problema anterior, completa la siguiente tabla: ¿Cómo encontraste el precio de 3 dulces? ¿Cómo encontraste el precio de 10 dulces?
A continuación, se presentan algunas respuestas.
Figura 1
La figura 1 es representativa de un tipo de procedimiento en el que las dos cantidades se correlacionan en función del número de casillas que se deben completar con los precios de los dulces, para este caso, cuatro. Así entonces, contar de 2 en 2 (desde el 120 hacia atrás) permite tener una distribución regular de los valores de los dulces de acuerdo con el número de casillas que hay que llenar. El 2 como base para el conteo seguramente proviene del hecho que las casillas contiguas a la cantidad 8 dulces tienen dos unidades más o dos unidades menos.
Figura 2
En procedimiento mostrado en la figura 2, si bien se parece al anterior, tiene la diferencia de que el conteo se basa en suponer un valor hipotético para cada dulce, y se realiza un conteo iterado de este valor hipotético tantas veces como cantidad de casillas vacías hay por llenar, y, además, se busca que la distribución de valores haga coincidir a la cantidad de 8 dulces el valor de $120. Nótese que el valor de $40 asignado a los 2 dulces da a entender que para esta casilla se tomó en consideración que el valor de 2 dulces es el doble del valor supuesto para un dulce, pero a partir de ahí se asumió que una casilla más era una dulce más, y no se consideró que el valor escrito en cada casilla de la primera columna es la cantidad de dulces al cual se le debía calcular el precio.
Desde la actividad matemática de los estudiantes, si bien los procedimientos no son correctos desde el punto de vista del procedimiento experto, sí lo es desde el punto de vista de los elementos que configuran la acción de los estudiantes: en relación con los objetos y de los conceptos, se evidencia que los estudiantes tienen una cierta noción de correspondencia biunívoca, en este caso, definida por la distribución espacial de los valores en la tabla suministrada (por supuesto, por esto es que desde el punto de vista del conocimiento experto, la solución no es correcta).
La tabla en la que se presenta la tarea a los estudiantes determina el tipo de análisis relacional que hacen: (1) hay dos columnas, una de la cuales se debe llenar con valores que se deben calcular, a saber, el precio de una cierta cantidad de dulces; (2) se asume que cada casilla vacía es un dulce más en la cantidad total de dulces, y por lo tanto, (3) para hallar el valor en dicha casilla, se agrega al valor en la casilla anterior, el valor de un dulce más. Nótese entonces que el instrumento usado para presentar la información determina la manera como los estudiantes analizan las relaciones entre las cantidades.
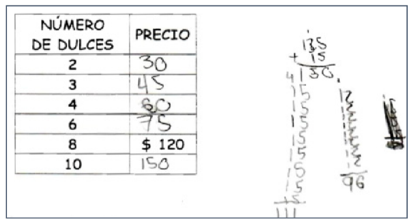Figura 3
La figura 3 muestra otro tipo de procedimiento el cual fija el valor hipotético para un dulce considerando que ese valor debe ser tal que 8 veces el mismo dé como resultado $120. Esta forma de proceder se ve con claridad en los cálculos que acompañan la tabla: se sumó 8 veces 12, y como no dio 120, se repitió el proceso ahora con 15. De igual forma se ve en la explicación verbal en la figura 21 en donde explícitamente se dice que se ha sumado 15 hasta completar 120.
Figura 4
Por su parte la explicación verbal que acompaña la tabla de la figura 4 es diferente, pues se basa en tomar el valor de 120 para calcular el valor de un dulce, haciendo reducciones sucesivas por la mitad, tanto del precio, como de la cantidad de dulces, siguiendo una forma de razonamiento por analogía (esto es, cualquier variación entre un par de cantidades en una magnitud, es traslada análogamente a las cantidades correspondientes en la otra magnitud). En ambos casos, el error en el valor asignado a 10 dulces muestra que, al final, se pierde de vista el asunto de la correspondencia cantidad de dulces–valor de dicha cantidad, mediada por la relación, un dulce cuesta 15 pesos.
De los anteriores fragmentos se puede inferir que los procedimientos de los estudiantes muestran cierta sensibilidad para percibir en un determinado evento el proceso de covariación entre las cantidades de los dos sistemas de cantidades involucrados en el evento, pero el criterio o regularidad usado para definir tal proceso de covariación no les permite la descripción precisa de lo que realmente sucede en el evento.
De estos procedimientos también se evidencia que los valores faltantes en la columna precio no se fijan de cualquier manera, sino que se hace a partir de un principio que tiene al menos dos momentos: uno, que fija el valor de un dulce (tomar como referencia que el valor de 8 dulces es $120), y otro, que permite hacer copias sucesivas de ese valor, tantas veces como dulces se tenga. Esto que implica interpretar el valor escrito en cada una de las casillas de la columna de la izquierda como la cantidad de veces que se debe repetir.
A manera de conclusión
Así pues, si los tres primeros procedimientos expuestos se pueden catalogar como procedimientos equivocados si se analizan sólo desde la perspectiva del conocimiento formal de las matemáticas, se llega a una conclusión clara: los estudiantes no saben multiplicar, aunque sí saben sumar. Sin embargo, cuando se analiza la lógica desde la cual fueron configurados dichos procedimientos, entendiendo dicha lógica con base en los instrumentos culturales disponibles para la acción (las tablas, su conocimiento sobre comprar y sobre las operaciones aditivas), se puede ver como lo realizado por estos tres estudiantes es correcto en un marco delimitado por la configuración de las tablas y la forma como se organiza la información en las mismas, pero basadas en el reconocimiento de una cierta forma de correlación entre las dos cantidades involucradas en la situación.
El último procedimiento muestra que los estudiantes de dichos grados sí pueden percibir los procesos de variación directamente proporcional, analizando como un cambio en una de las cantidades, tiene sus efectos análogos en la forma como cambia la otra cantidad, lo que en esencia es un análisis de covariación proporcional. Al comprender la actividad matemática de los estudiantes, como se dijo en la introducción, no en términos de deficiencias, sino en relación con lo que saben hacer, se pueden tomar decisiones importantes en la manera como el maestro puede orientar la actividad de enseñanza, con el fin de dirigir los procesos de aprendizaje de los estudiantes en un cierto sentido. RM
Referencias
1 Davidov, V. (1988). La enseñanza escolar y el desarrollo psíquico, Investigación psicológica teórica y experimental (M. Shuare, Trad.). Moscú: Editorial Progreso.
2 Leontiev, A. N. (1978). Activity, consciousness, and personality. New Jersey, NJ: Prentice-Hall.
Ricoeur, P. (2001). Del texto a la acción. Ensayos de hermenéutica II (P. Corona, Trad. 1.a ed.). Argentina: Fondo de Cultura Económica.
3 Obando, G. (2015). Sistema de prácticas matemáticas en relación con las Razones, las Proporciones y la Proporcionalidad en los grados 3.º y 4.º de una institución educativa de la Educación Básica. (Tesis Doctoral), Universidad del Valle, Cali, Colombia.
4 Stetsenko, A. (2005). Activity as object-related: resolving the dichotomy of individual and collective planes of activity. Mind, Culture, and Activity, 12(1), 70-88. doi: 10.1207/s15327884mca1201_6.
5 Radford, L. (2008). The ethics of being and knowing: Towards a cultural theory of learning. En L. Radford, G. Schubring & F. Seeger (Eds.), Semiotics in Mathemathics Education: Epistemology, History, Classroom, and Culture (pp. 215-234). Rotterdam: Sense Publishers. Radford, L. (2010). Algebraic thinking from a cultural semiotic perspective. Research in Mathematics Education, 12(1), pp. 1-19. doi: 10.1080/14794800903569741
6 Radford, L. (2013). Three key concepts of the theory of objectification: knowledge, knowing, and learning. Journal of Research in Mathematics Education, 2(1), 7-44. doi: 1 0.4471/redimat.201 3.1 9 Rajeswara, S. (2002).
7 Radford, L. (2006). Elementos de una teoría cultural de objetivación. Revista Latinoamericana de Investigación en Matemática Educativa, Número especial, 103-120.
