La recontextualización del discurso primario (el de un campo de producción disciplinar) y su concreción en un discurso secundario (el discurso que se construye en el contexto de las aulas), es lo propio, anota Bernstein, del fenómeno que ocurre cuando se trata de “comunicar” un determinado “conocimiento” en los contextos de la educación escolarizada. “Transposición didáctica”, a su vez, ha denominado Chevallard (2005) a este proceso 1 . Pero es un dilema y una incertidumbre para los investigadores en el campo de la educación identificar las sustancias de contenido que prevalecen en los discursos orales de los docentes y los estudiantes en los espacios cerrados de las aulas.
La escuela es un dispositivo cultural y político, de control simbólico y, en consecuencia, productora de tensiones. Para Bernstein “la teoría de la instrucción es un discurso recontextualizado crucial ya que regula los ordenamientos de la práctica pedagógica” (1990, p. 134). Recontextualizar es traducir el discurso -de un campo disciplinar, por ejemplo- a otro discurso, como el que se configura en las aulas. En esta perspectiva, dos situaciones ameritan la reflexión:
| 1 _________________________________________________________________________________________________________________Para el trabajo en el aula los maestros atienden solo los contenidos que el Ministerio selecciona, luego hay aquí una doble recontextualización: la que realiza la agencia gubernamental (el Ministerio y los currículos que diseña) y la del agente de la instrucción (el maestro); así, el de la instrucción realiza en aula una recontextualización de la recontextualización, al constreñirse a reproducir el discurso oficial propio del currículo declarado -por ejemplo, para el caso de Colombia, asumir pasivamente los “Derechos Básicos de Aprendizaje” (MEN, 2016) y las “Mallas de Aprendizaje (MEN, 2017)-. Así, la “planeación” del maestro es una forma de legitimación del currículo etnocentrista; dicha planeación también ha recontextualizado los contenidos seleccionados por la agencia gubernamental. Aquí se identifica una línea de investigación poco explorada: cómo se configura la recontextualización de la recontextualización en la “planeación” que realizan los docentes. |
| 2 _________________________________________________________________________________________________________________Los maestros se apoyan en el discurso primario (fuentes relacionadas con la matemática, por ejemplo) y en los documentos ministeriales de carácter general, que proporcionan señales sobre las competencias fundamentales en cada ciclo, como los lineamientos curriculares (1998) y los estándares básicos de competencias (2006), cuya organización no es la propia de un currículo taxativo y compartimentado, lo cual implica que el docente construya el currículo, sin perder de vista aquellos lineamientos y estándares. |
En ninguno de los dos casos el discurso pedagógico garantiza la aprehensión inmediata del conocimiento “propiamente científico” –el que está representado en fuentes primarias, por las que ha pasado el docente en su formación universitaria-, pues este se construye, como ocurre con todo conocimiento, en tiempos y espacios indeterminados y según las diversas experiencias intelectuales del sujeto deseoso de aprender 2 . El discurso pedagógico, si tiene efecto, provoca, induce, inquieta, seduce y hace sentir la necesidad de indagar en torno a un determinado conocimiento; tal discurso, cuando propicia interacciones, re-potencia la intuición (Not, 1983); se trata del conocimiento en el contexto escolar, en el sentido de un conocimiento que ha sido pedagogizado; de allí la importancia de hablar de la matemática escolar, de las ciencias sociales escolares, de la química escolar… Se trata de conocimientos escolares, que han sido previamente seleccionados, en el contexto escolar. Entonces la escuela ha de ser un dispositivo provocador hacia la necesidad del conocimiento científico a partir del conocimiento escolar.
 Los registros, según Halliday
Los registros, según Halliday
Halliday (1982) explica que la confrontación de registros es propia de los aprendizajes escolares. La categoría registro, tal como la propone Halliday, sirve para caracterizar las actuaciones discursivas de los estudiantes cuando frente a una determinada consigna eligen el registro según su propia experiencia, la que desearían comunicar, aunque no se corresponda con aquello que la consigna demanda:
Lo que constituye un registro son los significados, incluso los estilos de significación y los modos de argumentación, más que las palabras y las estructuras como tales. Con el fin de expresar nuevos significados, podría ser necesario inventar nuevas palabras, pero existen muchos modos distintos en que un lenguaje puede incorporar nuevos significados, e inventar nuevas palabras es apenas uno de ellos. No debe considerarse un registro matemático como algo integrado únicamente por la terminología, ni el desarrollo de un registro simplemente como un proceso de adición de nuevas palabras. (Halliday, 1982, p. 254).
Los registros son pues sustancias de contenido que el pensamiento produce cada vez que el sujeto interpreta en un contexto que reconoce. Los niños hacen grandes esfuerzos para entronizar con los contextos que subyacen en los textos que leen; el reto de la escuela es saber seleccionar los textos de tal manera que propicien las interacciones y, en la medida de lo posible, neutralizar la artificialidad en la que suelen caer los discursos en el aula; esta posibilidad, la de jugar, por ejemplo, con los números y con las notaciones formales en la resolución de problemas, la del asombro de saber descubrir el funcionamiento de una regla o una fórmula, esto es, la asimilación del registro “especializado”, constituye el punto de partida de un proceso que nunca se cierra.
Lo que se representa en el cuaderno o en las respuestas de las pruebas externas, son un punto de referencia para caracterizar estas maneras auténticas de los niños por construir los registros más allá de los prevalecientes en las aulas; muchas veces son registros sincréticos surgidos de la combinación entre los códigos escolares y los códigos que, en la vida práctica, el niño se inventa para saber afrontar una situación. Cuando los estudiantes asumen con responsabilidad la complejidad de las tareas, le apuestan a varios caminos para solucionar problemas utilizando incluso sistemas de representación no canónicos; el dilema está en la aceptación o no, por parte del docente, de las rutas elegidas por el estudiante. En todo caso, el planteamiento de Halliday ayuda mucho a la construcción de una epistemología para la práctica pedagógica:
Sería un error suponer que el lenguaje de las matemáticas (por lo cual se entiende el registro matemático, la forma de lenguaje natural utilizado en matemáticas y no su simbolismo matemático) es enteramente impersonal, formal y exacto; por el contrario, en él hay mucho de metáfora e incluso de poesía, de modo que es precisamente allí donde residen con frecuencia las dificultades. Expresiones como “seis menos cuatro dos” representan modos esencialmente concretos de significación que adoptan un aspecto metafórico cuando se utilizan para expresar relaciones abstractas y formales (esto es, cuando se interpretan como “6 – 4 = 2”). (Halliday, 1982, p. 263).
Los lenguajes se construyen con sistemas de convenciones y la matemática, como toda ciencia, tiene su propio sistema, es decir, su gramática específica, su modo de funcionar y de producir conocimiento, pero en dicho sistema nada es exacto; se interpretan representaciones, formales o lingüístico-discursivas.
Las representaciones
Los ejemplos siguientes son tomados de los resultados de las pruebas de matemática en el proyecto SERCE del LLECE-OREALC-UNESCO 3 , aplicadas en el año 2006 a niños de tercero y sexto grado, de escuelas de 16 países de América Latina. Una de las preguntas es la siguiente: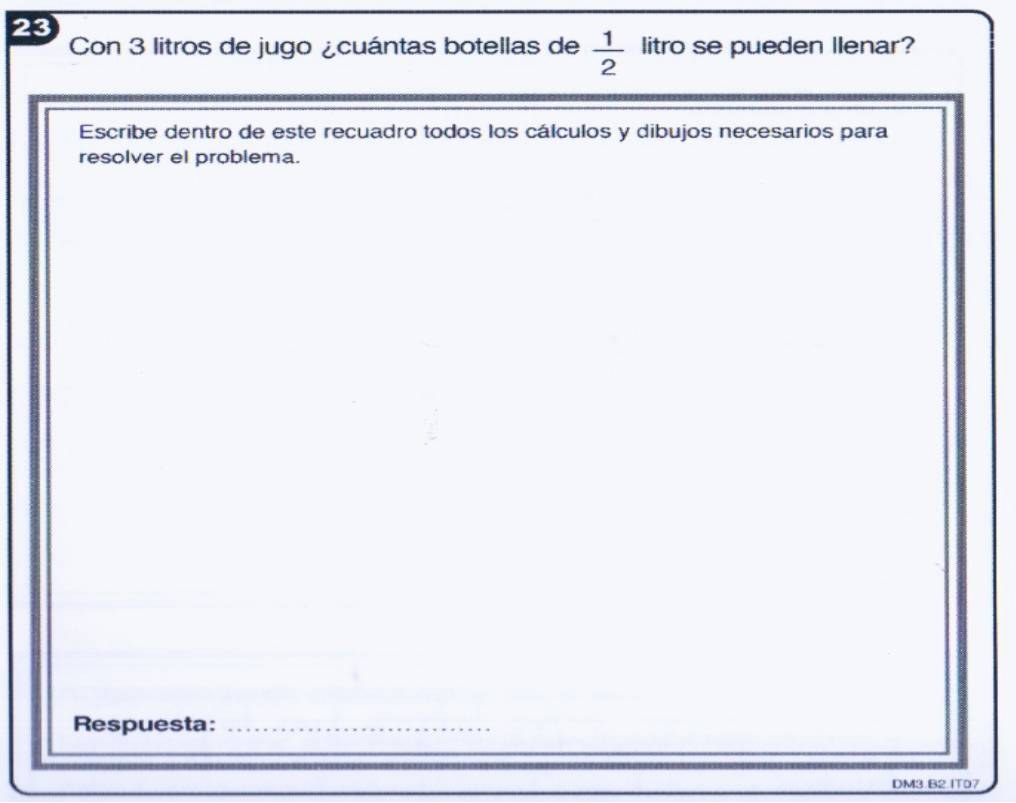
Se trata de una pregunta sobre el “dominio numérico”,cuya tarea es “resolver un problema que involucra el concepto de fracción” (SERCE, 2008, p. 49); la consigna está destinada a los niños de tercer grado. Es una pregunta abierta, es decir, el estudiante tiene que producir un texto para exponer la solución al problema. Algunas respuestas correctas son las siguientes:
 Figura 2 (SERCE, 2008).
Figura 2 (SERCE, 2008).
El estudiante recurre a la iconicidad figurativa (representación visual de las cosas), uniendo con una línea en arco cada dos botellas, marcadas estas con otra línea en la superficie, y luego expone la representación formal: 2·3 = 6; después explica lingüísticamente: “se pueden llenar 6 botellas de ½ L”. La representación icónica (el dibujo) le permite al niño asegurar la respuesta, como forma de comprobación empírica. Se identifican aquí tres tipos de representación: la icónica-visual, que proviene de la experiencia práctica; la formal, que proviene de la experiencia escolar, y la propiamente lingüística, modelada también por la experiencia escolar. Para llegar al conocimiento formal, o representación formal, el niño reconstruyó el conocimiento empírico, representado icónicamente; luego da el paso de los objetos a los signos propiamente convencionales (2 · 3 = 6, y su traducción al sistema lingüístico). Los registros “litro” y “½ litro” han sido aprehendidos por el estudiante, con la mediación del conocimiento intuitivo 4 . Otro caso es el siguiente:
 Figura 3 (SERCE, 2008).
Figura 3 (SERCE, 2008).
El estudiante también recurre a la representación icónica: dibuja tres botellas de un litro, procede a dividir en dos cada botella y luego enumera las partes; cuenta desde el uno y le da como resultado 6; luego lo enuncia combinando lo lingüístico con lo numérico: “En total me queda 6 de 1/2”; aunque solo dibuje 3 botellas, y no 6 como en el caso anterior, da cuenta de la respuesta; es otro modo de operar con los registros “litro” y “medio litro”, asociados con el referente de la botella de un refresco; sabe pues que las botellas de refresco son de un litro (conocimiento empírico, que proviene de la experiencia extraescolar) y desde allí realiza la operación. Otro niño dibuja seis recipientes y los identifica con medio litro cada uno:
 Figura 4 (SERCE, 2008).
Figura 4 (SERCE, 2008).
Para este estudiante no importa que cada recipiente no se parezca a una botella (puede ser una lata de jugo o de refresco), lo que importa es el modo de operar para resolver el problema. En el espacio de la respuesta introduce un término que proviene del sociolecto en su país: se denomina “pomos” a las bebidas con sabor a frutas. Ha recurrido pues al registro más común en la lengua práctica cuando se habla de botellas o de litros, pero igualmente recupera el conocimiento escolar con la convención ½, escrito en la superficie de cada recipiente. En este caso los recipientes son de medio litro, tal como se propone en la consigna. En otros casos el dibujo es algo meramente accesorio:
 Figura 5 (SERCE, 2008).
Figura 5 (SERCE, 2008).
La solución es explicada lingüísticamente, nada aporta el dibujo de las botellas. Es decir, explica de manera verbal lo que otros niños representan con dibujos. Aquí se trata de mitades (la de cada botella); considera innecesario dibujar dichas mitades, las que representa en su pensamiento y que escribe; se colige un nivel de abstracción mayor que en los casos anteriores, aunque no acuda a la formalización ni dibuje las seis botellas de medio litro. El registro “litro” está tácito con el registro “botella” pero lo hace explícito en la respuesta: “6 seis de medio litro.” En todas las respuestas aquí representadas, válidas en su estructura, “es interesante observar las distintas aproximaciones a la idea de mitad. En algunos casos es explícita la división de la botella de 1 litro en dos partes; mientras que en otras, el alumno asume que con dos medios litros se forma un
litro; o suma los medios hasta obtener 3, operación que probablemente, haya realizado reuniendo ½ + ½ = 1”. (Bronzina, et. ál., 2008, p. 51):
 Figura 6 (SERCE, 2008).
Figura 6 (SERCE, 2008).
De otro lado, un niño acude a la suma y aunque introduce la notación 6 en su respuesta, se observa que “no puede atribuir ningún significado a la escritura ½ y considera los números naturales que aparecen en el enunciado, respondiendo a un contrato frecuente para la resolución de problemas en el ámbito de la escuela” (Bronzina, et. ál., 2008, p. 51); es algo así como decir: “hay que usar todos los números del enunciado y hacer alguna cuenta con ellos para obtener la respuesta.”. (Bronzina et. ál., p. 52):
 Figura 6 (SERCE, 2008).
Figura 6 (SERCE, 2008).
En todos los casos hay una lógica particular que los niños construyen para resolver problemas como el que se plantea en esta prueba. Pero en las aulas se espera un único modelo para responder: el que fue enseñado. De otro lado, los ejemplos ilustran el carácter semiótico que cubre el proceso de recontextualización dado en la consigna, que propicia la heterogeneidad en el modo de responder. No es el conocimiento puramente matemático el que los niños construyen, es el juego con el lenguaje de la matemática en el contexto del conocimiento escolar lo que se representa en los casos analizados. Este juego se inscribe en un proceso de negociación de significados y es lo que se esperaría en las aulas cuando se asume el socio-constructivismo como un enfoque pedagógico y sociocultural (D´Amore, Radford y Bagni, 2007). RM
Referencias
1 “El trabajo que transforma de un objeto de saber a enseñar en un objeto de enseñanza, es denominado la transposición didáctica” (Chevallard, 2005: 45).
2 A su modo, Chevallard dice que “comúnmente, el saber enseñado vive muy bien encerrado sobre sí mismo, en una plácida autarquía, protegido por lo que hemos llamado la clausura de la conciencia didáctica –este distanciamiento, tan eminentemente funcional, del resto del mundo” (2005, pp. 25-26).
3 Segundo Estudio Regional Comparativo Explicativo de la Calidad de la Educación (SERCE) del Laboratorio Latinoamericano de la Evaluación de la Calidad de la Educación (LLECE), coordinado desde la oficina de
UNESCO en Santiago de Chile.
4 Dice Not: “… llamaremos intuición (del latín intuitio, imagen reflejada en un espejo) a la representación de las
realidades concretas que pueden expresar las formas matemáticas. En un sentido la intuición capta formas simbólicas mientras que el formalismo combina signos…” (1983, p. 276).
Bernstein, B. (1990). La construcción social del discurso pedagógico. Bogotá,: El Griot. Bishop, A. (1999). Enculturación matemática. La Educación Matemática desde una perspectiva cultural. Barcelona:, Paidós.
Bronzina, L., et. aál. (2009). Aportes para la ensenanza de la matemática. Santiago,: LLECE-SERCE-UNESCO.
Chevallard, I. (2005). La transposición didáctica. Del saber sabio al saber ensenado. B. Aires,: AIQUE.
D´Amore, B.; Radford, L.; Bagni, G. (2007). Obstáculos epistemológicosy perspectiva socio-cultural de la matemática. Cuadernos del Seminario en Educación, N.o 10. Instituto de Investigación en Educación. Bogotá: Universidad Nacional de Colombia.
Halliday, M. A. K. (1982). El lenguaje como semiótica social. México,: Fondo de Cultura Económica.
Ministerio de Educación Nacional (1998). Lineamientos curriculares. Matemática. Bogotá,: MEN.(2006). Estándares básicos de competencia. Bogotá,: MEN
Not, L. (1983). Las pedagogías del conocimiento. México,. F. C. E.
SERCE-LLECE-UNESCO (2008). Aportes para la ensenanza de la matemática. Santiago,: LLECE-SERCE-UNESCO-OREALC.