
Valentín, 5 años.
Cuenta sus propios dedos, los dibuja y los representa simbólicamente. A partir del 1, advierte que el espacio es insuficiente y decide continuar en la parte inferior en forma lineal.
La Neurociencia Educacional (NE) es una interdisciplina emergente que busca fundamentar científicamente las prácticas educativas y enriquecerlas. La relación entre Neurociencia y Educación no está libre de intensos debates en los que se distinguen, por un lado, autores reticentes a estrechar vínculos e incrédulos acerca de los posibles aportes de la ciencia 1 y, por otro, optimistas que aseguran que educadores, psicólogos y neurocientíficos pueden explicar el desarrollo de competencias desde diferentes niveles de análisis 2 y vincular las diferentes dimensiones en forma dinámica para evitar un abordaje reduccionista de su complejidad.
En los últimos años, ha crecido el número de investigaciones orientadas al estudio de la cognición numérica en busca de explicaciones sobre la base neurobiológica del procesamiento del número y el cálcuLa Neurociencia Educacional (NE) es una interdisciplina emergente que busca fundamentar científicamente las prácticas educativas y enriquecerlas. La relación entre Neurociencia y Educación no está libre de intensos debates en los que se distinguen, por un lado, autores reticentes a estrechar vínculos e incrédulos acerca de los posibles aportes de la ciencia y, por otro, optimistas que aseguran que educadores, psicólogos y neurocientíficos pueden explicar el desarrollo de competencias desde diferentes niveles de análisis y vincular las diferentes dimensiones en forma dinámica para evitar un abordaje reduccionista de su complejidad 3.
En los últimos años, ha crecido el número de investigaciones orientadas al estudio de la cognición numérica en busca de explicaciones sobre la base neurobiológica del procesamiento del número y el cálculo, los procesos cognitivos generales y específicos implicados en su adquisición y desarrollo o las particularidades de sus dificultades. Este empuje por parte de la neurociencia y la psicología cognitiva abona el “lado optimista” e impulsa fuertemente la traducción de los conocimientos validados en propuestas interdisciplinarias de intervención, por ejemplo…
- Las investigaciones sostienen que nacemos con una predisposición natural para la matemática y que sobre esta capacidad adaptativa se construyen los futuros aprendizajes a través de la influencia educativa. Es decir, contamos con un sistema de aproximación numérica (ANS) innato, rudimentario e independiente del lenguaje y de la enseñanza explícita que permite manipular magnitudes numéricas por medio de representaciones no simbólicas. Este sistema intuitivo (informal) sustenta la matemática formal (escuela) mediada por el lenguaje simbólico y, por lo tanto, es considerado un predictor estable del desarrollo de las habilidades aritméticas.

¿Por qué este conocimiento es considerado un aporte que “revoluciona” el modelo teórico más consensuado en educación matemática?
La escuela ha adherido tradicionalmente al constructivismo piagetiano y la neurociencia cuestiona uno de sus postulados más conocidos: los niños inician su vida sin ninguna representación estable e invariante del número y el conocimiento matemático progresa lentamente como una construcción lógica, es decir, la enseñanza de los procesos lógicos y su organización es un prerrequisito para la adquisición del concepto de número alrededor de los 5 años.
- Los investigadores proponen una analogía para explicar la representación de los números en nuestra mente: la numerosidad se representa como una magnitud fluctuante similar a una “línea numérica mental” 4
en la que las cantidades se ordenan de izquierda a derecha en forma ascendente.
¿Por qué este conocimiento debería ser uno de los pilares conceptuales para el diseño de intervenciones didácticas?

La representación abstracta del número, su sentido, su significado es nuclear en el desarrollo del pensamiento matemático y del cálculo mental. Un niño activa áreas neurales específicas involucradas en la representación abstracta del número para estimar, por ejemplo, la posición del 27 en una recta numérica con un intervalo entre 0 y 100. También para ordenar series de números de acuerdo con un criterio porque debe comprender la relación entre esos números, compararlos y determinar su ubicación espacial; o si debe completar blancos con el número anterior y el siguiente de un número dado o determinar el patrón de una serie numérica para poder continuarla. El rendimiento en tareas vinculadas con esta línea mental numérica, es un buen predictor de desempeño académico y, además, un recurso para identificar estudiantes con dificultades de aprendizaje.
 S. 1º grado. Ed. Primaria. Regularidades a través de filas y columnas.
S. 1º grado. Ed. Primaria. Regularidades a través de filas y columnas.
 E. 1º grado. Ed. Primaria. Proyecto de Inclusión. Línea numérica con soporte. visual.
E. 1º grado. Ed. Primaria. Proyecto de Inclusión. Línea numérica con soporte. visual.
Estos hallazgos fundamentan el uso de la recta numérica como recurso más apropiado para acompañar la construcción de la línea mental abstracta. Si bien en la escuela coexisten las representaciones lineales y en tablas o cuadros numéricos, se ha extendido el uso de los cuadros hasta convertirse en el recurso más utilizado.
Estos cuadros se apoyan en la ubicación de los números ordenados por filas y columnas porque esta organización favorece el análisis de las regularidades del sistema decimal y la visualización de los cambios y continuidades de las distintas posiciones a medida que se avanza o retrocede en la serie.
- Además del sistema de aproximación numérica, la neurociencia y la psicología cognitiva describen un sistema de representación verbal exacto que se activa de diferentes maneras de acuerdo con la demanda de la situación: para conjuntos pequeños (subitización) y para conjuntos grandes (conteo) 6.
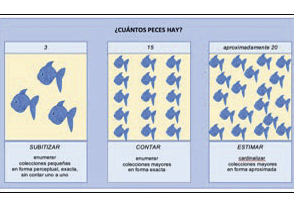
Los estudios sobre ANS concluyen que las diferencias individuales observadas en tareas de comparación de magnitudes se vinculan con las diferencias posteriores en el desempeño en aritmética 7. Y las investigaciones sobre el conteo evaluado en educación infantil sostienen que también es un predictor estable de las habilidades matemáticas en primaria 8.
La evidencia es muy contundente… pero, ¿cómo se podría reflejar en la escuela?
La nueva perspectiva requiere la reformulación de estrategias didácticas que contemplen la estimulación temprana, sistemática y explícita del sentido numérico desde nivel inicial.
El foco de la enseñanza no debería ser el número en función solo del cálculo sino la representación mental de la magnitud…comprender su significado en un determinado contexto para poder comparar espacios, tamaños o cantidades, o elaborar secuencias.
- Entonces… la información numérica se manipula mentalmente a través de tres tipos de códigos de representación 9:
- Representación analógica a las cantidades: representación semántica en la que los números se representan en la línea numérica. Se activa en tareas vinculadas con el significado del número: estimar, comparar, o calcular en forma aproximada.
- Representación verbal auditiva: los números se representan con una cadena de palabras organizadas sintácticamente. Se relaciona con las tareas de conteo y con las tablas de multiplicar.
- Representación en formato arábigo: se representa el número con una cadena de dígitos. Se utiliza para realizar operaciones multidígito.
La representación verbal y la arábiga no cuentan con la información semántica de la representación analógica. El código verbal (/cinco/) es el primero en adquirirse y sirve para la construcción del código arábigo (5) entre nivel inicial y los primeros años de educación primaria.
De acuerdo con los modelos de procesamiento de número cuando un estudiante escucha /doscientosonce/ y escribe “211” transcodifica información numérica, es decir, traduce de un formato verbal oral a un formato arábigo.
 F. 2º grado. Ed. Primaria. Dictado de números. El colorado corresponde a la corrección del educador.
F. 2º grado. Ed. Primaria. Dictado de números. El colorado corresponde a la corrección del educador.
Los registros numéricos tienen diferente sintaxis, el formato o código verbal es aditivo (200…11) y el arábigo es posicional. F. comete varios errores de tipo “sintácticos” cuando intenta traducir literalmente y yuxtapone porque todavía no aplica las reglas propias del sistema de numeración decimal, por ejemplo, 210028 por 228, y comete un error denominado “léxico” al escribir 299 por 239. Desde el punto de vista cognitivo, los errores léxicos se producen por una falla en la recepción, almacenamiento o recuperación de la información léxica, en cambio, los errores sintácticos se deben a un déficit en la producción arábiga independiente de la información léxica.
El desarrollo de la transcodificación numérica se caracteriza por ser un proceso muy fluctuante, marcado por rupturas, avances y retrocesos a medida que se presentan intervalos numéricos mayores… ¡cada nuevo rango desestabiliza el anterior!
¿Por qué estos conocimientos científicos son un aporte para fundamentar las intervenciones?
El signo de pregunta de la maestra de F. expresa el desconcierto ante su producción. No logra advertir la hipótesis del niño sobre cómo “se escriben los números”. El dictado de números es una práctica muy frecuente en la escuela, especialmente en los primeros años, pero a veces se “hacen porque siempre se hicieron” a pesar de ser un instrumento valioso para determinar los niveles de desarrollo de los procesos de transcodificación.
Las intervenciones educativas que promueven el desarrollo de competencias están siempre guiadas por el conocimiento preciso de los procesos generales y específicos que están involucrados en las diferentes tareas.
 J. 2º. Educación Primaria. Las consignas demuestran el desconocimiento de los procesos que están implicados en la ejecución de cada una de las tareas: transcodificación numérica y comparación numérica
J. 2º. Educación Primaria. Las consignas demuestran el desconocimiento de los procesos que están implicados en la ejecución de cada una de las tareas: transcodificación numérica y comparación numérica
Desde el lado “optimista” y a través de estos aspectos de la construcción del significado del número y sus formas de representación, se describieron conexiones posibles entre las conclusiones de las investigaciones y las prácticas de enseñanza.
El desafío para la Neurociencia Educacional será instrumentar los medios para lograr reciprocidad en el flujo bidireccional de información entre neurociencia y educación, traducir los aportes científicos en prácticas concretas y viables – tarea que debería ser asignada a profesionales formados sólidamente en ambos campos disciplinares- y considerar que la transformación en intervenciones pedagógicas pueda ser evaluada sobre la base de su efectividad en contexto 10.
En definitiva, la discusión no es si los conocimientos pueden o no ser traducidos sino cuáles son los contenidos que dan soporte sólido a la práctica educacional, cómo se van a transformar esos contenidos que romperán con la clásica matemática reproductiva basada en procedimientos, quiénes van a mediar profesionalmente en este proceso y cómo se van a comunicar en forma efectiva. Sin dudas, el reto es enorme y hasta ahora los avances son lentos y con muchos obstáculos, pero tal vez éste es el camino al que debemos seguir dedicados. RM
Referencias
1 Bowers, Jeffrey S. (2016). The practical and principled problems with educational neuroscience. Psychological
Review, 123, 600-612.
2 Howard-Johnson P., Ansari, D., De Smet, B., Laurillard, D., Varm, Butterworth, B, Goswami, U. Thomas, M. (2016). The principles and practices of educational neuroscience: Comment on Bowers. Psychological Rewiew,123, 600-627
3 Benarós, S., Lipina, S., Segretin, M., Hermida, M., Colombo, J. (2010). Neurociencia y educación: haca la
construcción de puentes interactivos. Rev Neurol, 50 (3):179-18
4 Halberda, J. Mazzocco, M., Felgenson, L. (2008). Individual differences in non-verbal number acuity correlates
with math achievement. Natures, 455(7213):665-8 Dehaene S. (2011). The number sense: How the mind creates mathematics. New York: Oxford University Press
6 Baroody, A. J., Purpura, D. J., Eiland, M. D., & Reid, E. E. (2015). The impact of highly and minimally guided discovery instruction on promoting the learning of reasoning strategies for basic add-1 and doubles combinations. Early Childhood Research Quarterly, 30, 93–105.
7 Leibovich, T., & Ansari, D. (2016). The symbol-grounding problem in numerical cognition: A review of theory, evidence, and outstanding questions. Canadian Journal of Experimental Psychology, 70, 12-23.
8 Leibovich, T., & Ansari, D. (2016). The symbol-grounding problem in numerical cognition: A review of theory, evidence, and outstanding questions. Canadian Journal of Experimental Psychology, 70, 12-23.
9 Dehaene S, Cohen L. Toward an anatomical and functional model of number processing. Mathematical Cognition.1995; 1, 83-120
10 Dehaene S, Cohen L. Toward an anatomical and functional model of number processing. Mathematical Cognition.1995; 1, 83-120.





