Incluso las voces más radicales que proponen, de manera bastante irresponsable, que del currículo escolar desaparezcan todas las disciplinas, y queden solamente las horas de recreo, de convivencia y crecimiento de la tolerancia, de formación ciudadana, y algún espacio para el desarrollo del pensamiento y la lectura crítica, incluso esas voces reconocen que las matemáticas tienen un papel importante que jugar en la vida escolar. No se ponen de acuerdo en cuáles matemáticas enseñar, pero aceptan que de alguna u otra manera deben estar presentes, palabras más, palabras menos, “por ser un herramienta indispensable en la vida de cualquier ciudadano”.
Y en efecto, las matemáticas son una herramienta indispensable en la vida de cualquier ciudadano, pero no es solamente por serlo que deben estar presentes en la vida escolar, ni ello lo que nos oriente a la hora de decidir cuáles son esas matemáticas que todos deben saber, entender o dominar. Los minimalistas consideran que un poco de aritmética, es decir, el manejo adecuado y preciso de los números enteros, alguna competencia con las fracciones, los números decimales y porcentajes, y aplicar la célebre “regla de tres” (Si cuatro panes me cuestan $3.600, ¿cuánto me costarán nueve panes?), basta y sobra. Otros minimalistas, pero que no lo son tanto, consideran que, además de lo anterior, no sobraría empapar a los estudiantes con algunos rudimentos del álgebra, y de unas nociones de la geometría, reconocer puntos, líneas, círculos, cuadrados y triángulos, y saber las recetas para hallar áreas y perímetros, pero sin llegar jamás a torturarlos mostrándoles demostraciones, y menos exigiéndoselas.
Los tradicionalistas, por su lado, insisten en que las matemáticas deben seguir enseñándose como una disciplina independiente de todas las demás, a las que se les dediquen en la escuela muchas horas silenciosas, y otras tantas en el hogar, llenando páginas de ejercicios, muchos ejercicios y mucha práctica. Ellos, los tradicionalistas, conciben su labor de profesores de matemáticas como proveedores de esas herramientas indispensables que todo ciudadano debe poseer para poder funcionar, algo así como un kit que todos debemos cargar a todos lados para cuando se pueda ofrecer. En lo que los tradicionalistas no se pueden poner de acuerdo es en lo que ese kit debe llevar, pero más o menos el consenso es que incluya bastante aritmética, una buena cantidad de geometría (pero sin muchas demostraciones que atolondren a los estudiantes), mucha álgebra manipulativa, alguna competencia en el manejo de datos, cierto feeling por la trigonometría, y un toquecito de lo que hoy se conoce como precálculo. Un kit dotado de todo esto, se ufanan los tradicionalistas, les permite a los estudiantes desempeñarse decorosamente en las Pruebas Saber e ingresar a la universidad sin problemas. Y tienen razón, ese kit, si los estudiantes lo adquirieron no del todo de manera memorística, si algo entendieron de lo que sucedía cuando lo estaban copiando en sus cuadernos, basta para responder buena parte de la pruebas de matemáticas de los exámenes de estado. No son, sin embargo, herramientas indispensables que toda persona deba poseer para funcionar como ciudadano. Pasadas esas pruebas, si no tienen necesidad de seguir estudiando matemáticas, en poco tiempo buena parte de esos estudiantes comenzaran a perder, olvidar, la mayoría de la herramientas del kit: olvidarán todos los casos de factorización, la ecuación cuadrática, el volumen del cilindro, el binomio de Newton, y ya no recordarán cuál era el propósito ni la manera de hallar la media, moda y mediana de una colección de datos. Y sin embargo, esos estudiantes olvidadizos, ya sin nada o poco del kit original, se convertirán en ciudadanos, votarán, leerán encuestas y las interpretarán a su gusto, pagarán impuestos, comprarán carro y vivienda, tendrán tarjetas de crédito, viajarán y se jactarán de que “las matemáticas no es lo mío”. A pesar de haberse quedado sin nada de lo que venía en el kit, se desempeñan como ciudadanos más o menos competentes, y lo hacen porque en el camino, por accidente, por instinto de supervivencia, por azar o de alguna otra forma, aprendieron a pensar, así sea a medias. Las matemáticas son esenciales en la vida escolar, no por ser un herramienta, sino porque enseñan a pensar. Todas las disciplinas lo hacen: la historia, la literatura, la ciencias naturales, la educación física, todas enseñan, o deberían enseñar a pensar, pero ninguna lo hace de una manera tan efectiva ni inmediata como las matemáticas. No hay pensamiento más crítico, para darle el nombre de moda, que el pensamiento matemático. Ya lo decía Ernesto Sábato en Uno y el universo:
“Existe una opinión muy generalizada según la cual la matemática es la ciencia más difícil, cuando es la más simple de todas. La causa de esta paradoja reside en el hecho de que, precisamente por su simplicidad, los razonamientos matemáticos equivocados quedan a la vista. En una compleja cuestión de política y arte hay tantos factores en juego y tantos desconocidos e inaparentes, que es muy difícil distinguir lo verdadero de lo falso. El resultado es que cualquier tonto se cree en condiciones de discutir sobre política y arte –y en verdad lo hace– mientras que mira la matemática desde una respetuosa distancia”.

Entonces, ¿por qué tantos huyen de las matemáticas? ¿Por qué tantos las odian y las padecen? ¿Por qué los profesores universitarios se quejan cada vez más de lo mal preparados matemáticamente que llegan los estudiantes a sus aulas? La razón, como la matemática, es simple. Estamos enseñando la matemática que no es, para lo que no es, y como no es.
Sí, todo bachiller, todo ciudadano, debería ser capaz, en cualquier momento de su vida, calcular cuál de dos préstamos para comprar vivienda (o cualquier otra cosa) le conviene más, pero si no lo es, le queda la opción de consultar a alguien que sí lo sea. Es posible que en su kit alguna vez tuvo todas las herramientas relevantes para hacerlo: porcentajes, intereses compuestos y simples, tasas, etc., pero si por falta de uso estas se oxidaron, o perdieron del todo, no queda alternativa que consultarle a otro. Dependiendo de cómo haya sido su formación matemática, la ayuda que le ofrezca su consultor puede resultarle inteligible o no: podrá entender sus explicaciones, ponderarlas y decidir por sí mismo, o simplemente acatarlas. La diferencia estriba en si aprendió a pensar o simplemente a operar. Es incluso posible que no haya olvidado del todo las herramientas, que recuerde las fórmulas para hallar intereses, cuotas y capitales, pero si en su momento no las entendió, si no pensó con ellas, de nada le servirán en el momento de necesitarlas para tomar una decisión, y tendrá que dejar que otro lo haga por él.
Ya sea que sean pocas o muchas matemáticas las que les enseñemos a nuestros estudiantes, pasados los años esas matemáticas poco o nada les servirán si fueron simplemente una memorización de definiciones y fórmulas, y un adiestramiento en su ejecución y aplicación. Si no sirvieron para que los estudiantes aprendieran a pensar, a analizar, a tomar un problema y comprenderlo, desmenuzarlo, deshacerse de los distractores que seguramente lo acompañan, a buscar entre su kit las herramientas que le puedan ayudar a resolverlo (y si no las haya, a buscarlas en Google), a comprobar si su solución efectivamente resuelve el problema y, finalmente, a comunicar a otros su solución, argumentando su validez, entonces de nada sirvieron.
Pero para que las matemáticas sirvan para pensar no pueden seguir siendo “enseñadas”. “Enseñar” significa “mostrar”, y mostrar es lo que los profesores de matemáticas venimos haciendo hace muchos años: les mostramos a los estudiantes los doce o trece casos de factorización, la ecuación cuadrática, la derivada de un cociente, incluso el teorema fundamental del cálculo, y les prometemos que algún día todo ello les será de gran utilidad. Ese día nunca llega, y cuando a mediados de su primer semestre universitario algún profesor impertinente les pide que den un ejemplo de la derivada en la vida real, solo uno entre mil logra mencionar la velocidad de un vehículo o el índice de la inflación como ejemplos válidos, a pesar de que son capaces de derivar cualquier función compleja que les pongan por delante. “Mostradas”, las matemáticas no sirven para nada, y además de no servir para nada, no se puede apreciar su belleza. Tanto la utilidad y la belleza de las matemáticas están en los argumentos con que están construidas y en los que se sustentan. Esos argumentos no se “muestran” o “enseñan”, sino que se crean, se descubren, se desarrollan. Así como no se aprende a nadar viendo a otros nadar o explicando en el tablero cómo se hace, tampoco se aprende a pensar viendo a otros hacerlo. Para aprender a pensar, que es para lo que las matemáticas sirven, a los estudiantes hay que invitarlos a meterse en la piscina de las matemáticas, sus aguas previamente aclimatadas, y permitirles zambullirse a gusto en ella. La piscina de las matemáticas son sus teoremas, problemas, soluciones, acertijos, paradojas, conjeturas, demostraciones, argumentos, contraargumentos, falacias, intuiciones y sorpresas. El poder experimentarlas de primera mano, poder hablar de ellas y discutirlas, aun acaloradamente, con los compañeros, y no solo con el profesor, es lo que permitirá que los estudiantes finalmente descubran el maravilloso poder de las matemáticas y, de paso, su belleza. El matemático y educador Leon Henkin ya lo había advertido hace muchos años:

“Una de las grandes ideas falsas que tenemos sobre las matemáticas que practicamos en el salón de clase, es que el profesor conoce siempre la solución a todos los problemas. Esto les da a los estudiantes la idea de que existe un libro con todas las respuestas correctas a las preguntas interesantes y que el profesor las conoce todas. Si uno pudiese tener este libro, tendría todo resuelto. Esto es realmente todo lo contrario a la verdadera naturaleza de las matemáticas”.
Lo cierto, entonces, es que en la jornada escolar de todo estudiante debe haber, además de los que los “expertos en educación” contemporáneos reservan para la convivencia, la ternura, la felicidad, la ciudadanía y el recreo, espacios temporales y físicos para las matemáticas, unas matemáticas sólidas y rigurosas, con un profesor preparado profesionalmente tanto en la disciplina como en su didáctica, dispuesto a reflexionar permanentemente sobre su quehacer, a mantenerse al día en los avances de su ciencia (tanto teóricos como tecnológicos) y a permitir que sus estudiantes “hagan” matemáticas y no simplemente las miren. Esos espacios, por supuesto, no impiden que en ellos se pueda practicar todo lo demás: la historia, la lengua, la geografía, la colaboración, la convivencia, incluso la educación física (hay quienes pensamos mejor caminando o corriendo) y el recreo, como bien lo sabemos quienes hemos sido discípulos de Martin Gardner.
Si bien la discusión acerca de cuáles son esas matemáticas que mejor sirven para pensar es muy importante, no es lo esencial, además de que es difícil que dos educadores o matemáticos se pongan de acuerdo en ello, como bien ha quedado claro cuando los Ministerios de Educación los han convocado para que lo hagan. Hay cierto consenso de hacer coincidir las matemáticas escolares con su desarrollo histórico, pero por alguna razón sin tocar nada que no haya dejado ya organizado el gran Leonhard Euler (1707-1783) hace ya casi un cuarto de milenio. Pero cualesquiera que sean esas matemáticas que finalmente escojamos, debemos asegurarnos que aparezcan como unas matemáticas vivas, en constante evolución, repletas de problemas abiertos que lastimosamente nunca se mencionan en clase, de soluciones siempre mejorables, de controversias y ruido. Las matemáticas silenciosas, que solo hay que memorizar y repetir, la matemática de Baldor y de todos sus imitadores tuvo ya su cuarto de hora y seguirla practicando lo único que hace es daño.
Tres tipos de matemáticas
Matemáticas para memorizar y repetir (matemáticas minimalistas)
| 7 x 1 = | 9 x 1 = |
| 7 x 2 = | 9 x 2 = |
| 7 x 3 = | 9 x 3 = |
| 7 x 4 = | 9 x 4 = |
| 7 x 5 = | 9 x 5 = |
| 7 x 6 = | 9 x 6 = |
| 7 x 7 = | 9 x 7 = |
| 7 x 8 = | 9 x 8 = |
| 7 x 9 = | 9 x 9 = |
| 7 x 10 = | 9 x 10 = |
Matemáticas para manipular (matemáticas tradicionales)
Convierta estas ecuaciones cuadráticas a su forma de vértice y diga cuáles son sus vértices:
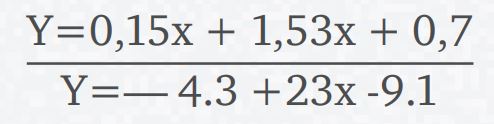
Matemáticas para pensar
Dos hermanos, Julián y Miguel, corren una carrera de 100 metros. Julián gana la carrera por 3 metros. Deciden correr la carrera de nuevo, pero en está ocasión Julián partirá 3 metros detrás de Miguel. Si en la segunda carrera ambos hermanos corren exactamente a la misma velocidad que corrieron en la primera, ¿cuál de los dos llega primero a la meta? RM





