La papiroflexia se puede emplear como un recurso para enseñar diferentes contenidos matemáticos, desarrollar habilidades sociales y estimular algunas de las inteligencias múltiples de Howard Gardner. Las inteligencias que se potencian cuando empleamos la papiroflexia dentro del aula serán: la lógico-matemática (geometría, resolución de problemas…), la espacial (manipulación mental de objetos), la corporal-kinestésica (precisión en los pliegues), la interpersonal (empatía para trabajar en grupo), la intrapersonal (trabajando con la frustración y la baja autoestima) y la lingüística (explicando a sus compañeros cómo se pliegan las figuras y haciéndose entender).
Podemos emplear la papiroflexia para finalidades tanto artísticas (convirtiéndose en auténticos Makers) como educativas (a través del juego) y utilizando un único papel o uniendo varios de igual forma sin pegarlos (construyendo “monstruos geométricos”) en lo que se denomina papiroflexia modular. Dentro de esta última tipología usaremos el módulo 4 de 2×1 y el módulo Sonobé del japonés Mitsunobu Sonobé con el cual mi alumnado de 13 a 17 años tiene amplia experiencia.
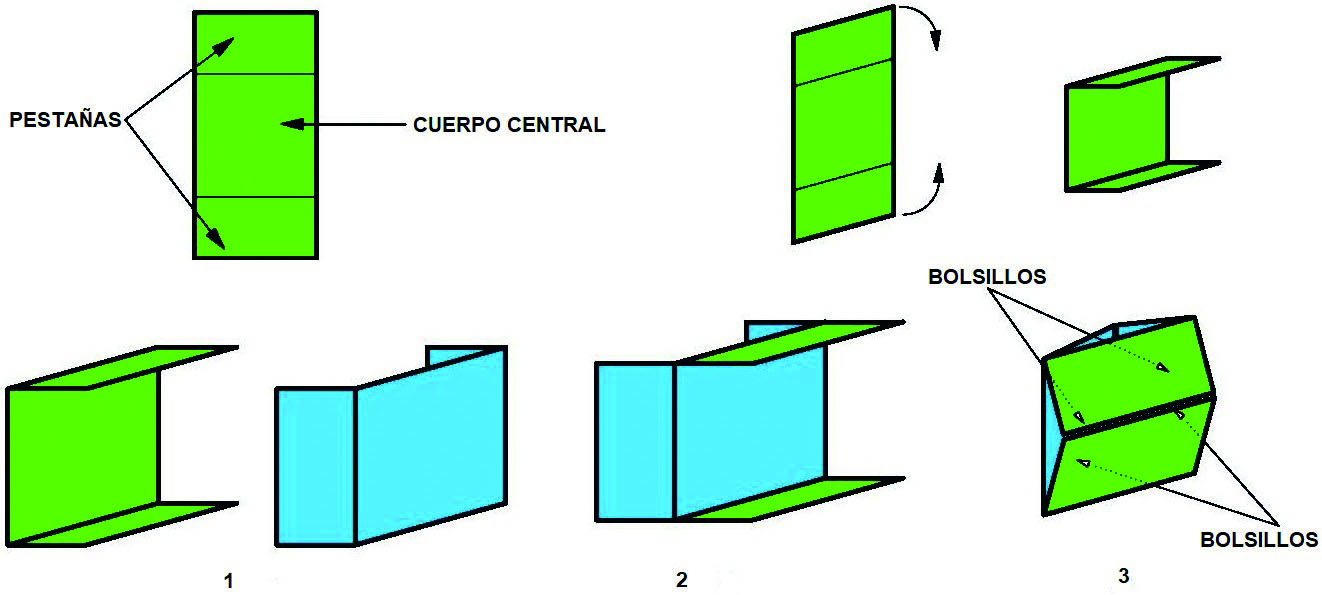módulo 4 de 2×1
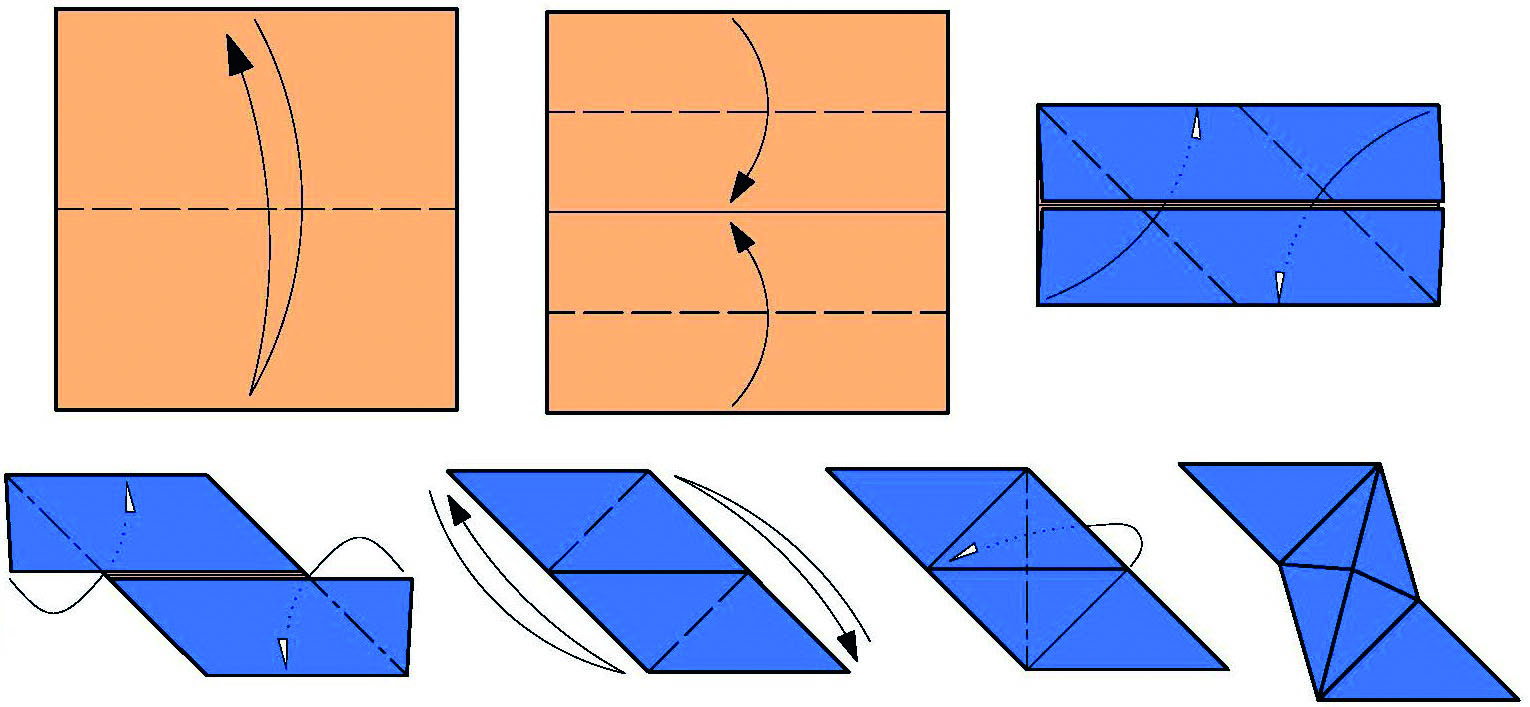módulo Sonobé
Una de las figuras más reconocidas y plegadas por los principiantes papirofléxicos es la conocida pajarita. Dentro del aula de matemáticas podemos trabajar diferentes conceptos mientras la estamos plegando como por ejemplo: tipos de triángulos, teorema de Pitágoras, áreas,…
Podemos proponer cuestiones del siguiente tipo:
1. Si partimos del cuadrado L x L de superficie L2 obtenemos una pajarita (plegando los vértices al centro) cuya superficie es la octava parte de la del cuadrado (L2/8).
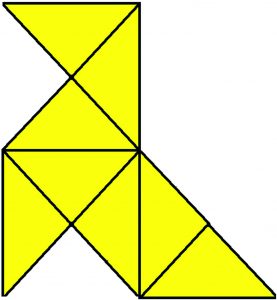(Nota: el área de la pajarita la consideramos como si fuese una figura en el plano).
Durante el curso académico 2016-17 les propuse a dos alumnos de 17 años: David Chao y Pablo García de 1.º Bachillerato del IES Pedro Floriani de Redondela (Pontevedra), que hiciesen un trabajo de investigación sobre las construcciones con regla y compás y que se centrasen en la “rebeldía” del heptágono para terminar plegándolo en clase.
Platón fue un gran divulgador del uso de la regla y el compás para las construcciones geométricas (con regla de longitud infinita y sin numeración, y compás que traza circunferencias y no traslada distancias). En el estudio de este campo los griegos se encontraron con 3 problemas: la cuadratura del círculo, la duplicación del cubo y la trisección del ángulo que no consiguieron resolver.
Podemos preguntarnos qué polígonos regulares se pueden construir con regla y compás. Existe un teorema enunciado por Gauss-Wantzel que determina esta posibilidad. Dice así:
“Un polígono regular de n lados, siendo n un número primo, es construible con regla y compás si y sólo si n -1 es una potencia de 2”.
Por lo tanto, los polígonos regulares de 3 y 5 lados son construibles con regla y compás, pero el de 7 lados no lo es porque 7 – 1 = 6 y seis no es potencia de 2. Teniendo en cuenta que los polígonos regulares de 4 y 6 lados tienen una construcción sencilla con regla y compás (investígalo), podemos afirmar que el heptágono es el primer polígono regular al que “no le gustan las reglas” (ni los compases).
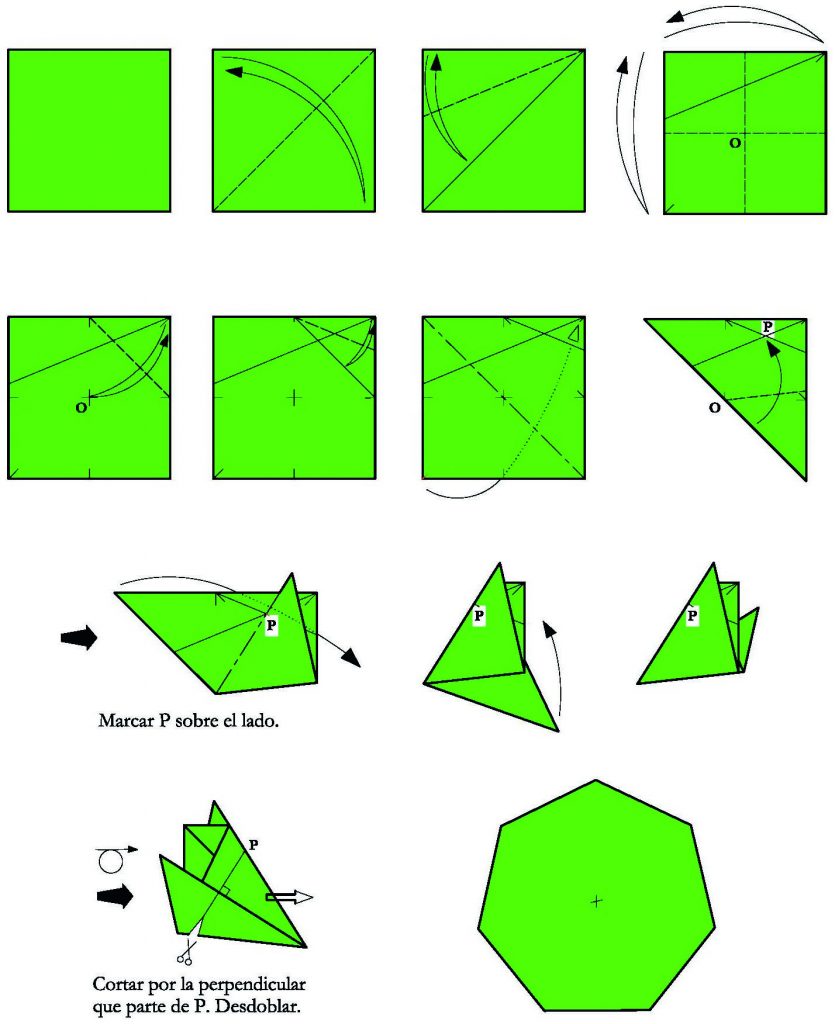
Mediante la papiroflexia tenemos varias formas de conseguir un heptágono. Una solución cuasiperfecta (y “sencilla”) la explica D. Jesús de la Peña en su libro Matemáticas y Papiroflexia de la AEP (Asociación Española de Papiroflexia) en el 2001.
Después de obtener el heptágono pudimos comprobar, utilizando conceptos trigonométricos explicados durante el curso, que el error entre el ángulo central real del heptágono y el obtenido mediante estos pliegues era inferior al 0,1%.
Construcciones modulares
- Antonio Vidal Pérez plegador, diagramador y amigo con el que comparto diferentes actividades origamistas desde hace algunos años, en febrero de 2011 diseñó un módulo papirofléxico sencillo a la vez que original que lo denominó módulo 4 de 2×1.
En vista de la practicidad de dicho módulo le propuse que le diésemos una utilidad pedagógica a su creación y entre los dos pensamos aplicaciones didácticas del mismo a las matemáticas como por ejemplo en el teorema de Pitágoras. Después de varios intentos pudimos comprobar que el módulo de Antonio era mucho más manejable que el Sonobé y procedí a llevar al aula este modelo papirofléxico de Antonio para construir otro tipo de proyectos. Para obtener este nuevo módulo se partirá de un papel cuadrado que cortaremos en 2 rectángulos iguales de proporciones 2×1 en los que la altura será el doble de la base.
Las siguientes demostraciones papirofléxicas del teorema de Pitágoras las presentamos sobre mosaicos construidos con unos 700 módulos 4 de 2×1.
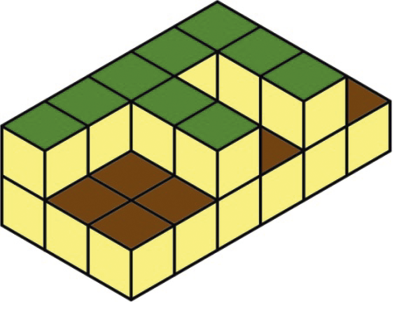
Demostración del teorema de Pitágoras sobre triángulo rectángulo isósceles:
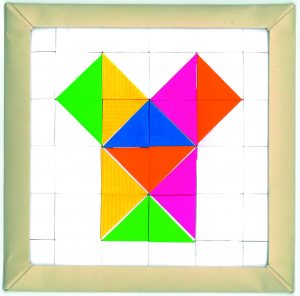
Como se puede ver en la construcción, la suma de las áreas de los 2 cuadrados construidos sobre los catetos del triángulo rectángulo isósceles de color azul del centro es igual al área del cuadrado construido sobre la hipotenusa (solo tenemos que fijarnos en las zonas coloreadas de los 3 cuadrados y ver que cumplen el teorema).
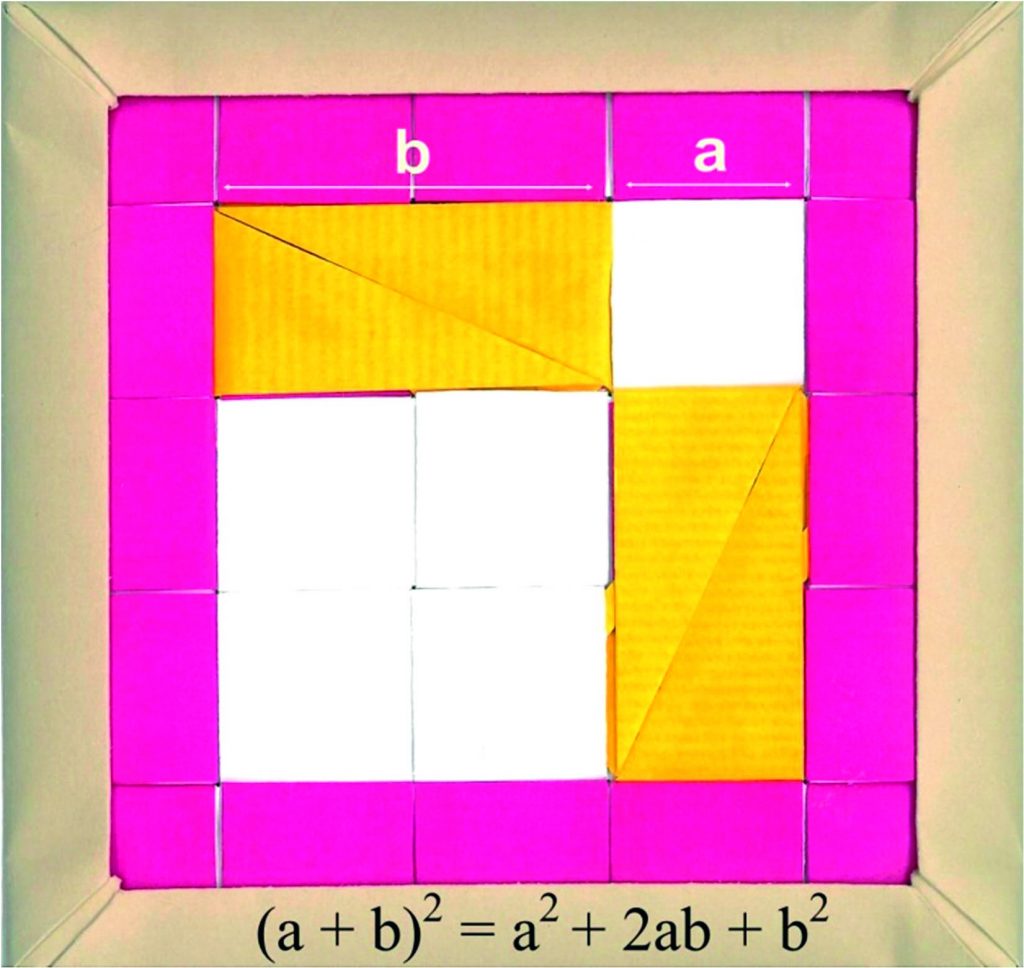
Demostración del teorema de Pitágoras sobre triángulo rectángulo escaleno:
Marco 1: Tenemos un triángulo rectángulo escaleno de color rosa de dimensiones 2×1 dentro de un cuadrado blanco cuyo lado es la suma de los catetos del triángulo.
Marco 2: En el interior del cuadrado azul hay un cuadrado blanco rodeado de 4 triángulos rectángulos amarillos iguales, cuyo lado es de la misma longitud que las hipotenusas de los triángulos amarillos (que son iguales al de color rosa del marco 1).
Marco 3: En el interior del cuadrado rosa también hay los mismos 4 triángulos rectángulos amarillos que en el marco 2 y también tenemos 2 cuadrados blancos construidos sobre los catetos de los triángulos amarillos.
Por tanto, concluimos que la suma las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado construido sobre la hipotenusa.
Veámoslo:
Las áreas interiores de los cuadrados azul marino y rosa son iguales a 9 u2 (marcos 2 y 3).
Como dentro del cuadrado azul hay 1 cuadrado blanco y 4 triángulos amarillos, y dentro del cuadrado rosa hay 2 cuadrados blancos y los mismos 4 triángulos amarillos; entonces, podemos concluir, una vez eliminados esos 4 triángulos amarillos, que:
El área del cuadrado construido sobre la hipotenusa del triángulo rectángulo amarillo es igual a las sumas de las áreas de los cuadrados construidos sobre los lados del mismo triángulo amarillo. Quedando así demostrado el teorema de Pitágoras.
También podemos aprovechar esta construcción modular papirofléxica para explicar el desarrollo del siguiente producto notable:
(a + b)2 = a2 + 2ab + b2
Veámoslo:
Área del cuadrado: (a + b)2. En su interior hay:
2 cuadrados blancos de áreas: a2 y b2 respectivamente.
2 rectángulos amarillos de áreas: 2·a·b
Por tanto, hemos demostrado la igualdad.
Es recomendable insistir en el aula en esta demostración pues el alumnado tiende a realizar esta operación:
(a + b)2 = a2 + b2
“Monstruos Geométricos”
Otras de las aplicaciones didácticas que fueron “saliendo” con los módulos 4 de 2×1 fue el fractal: “La curva de Hilbert” la cual nos permite explicar en el aula los procesos iterativos infinitos y analizar las propiedades de esta curva.
La curva de Hilbert es una curva fractal continua que recubre una región del plano descrita por el matemático alemán David Hilbert en 1891 que tiene la peculiaridad de ser una línea de dimensión 2.
La curva de Hilbert se genera en un cuadrado que se ha dividido en otros cuatro, cuyos centros se unen con una línea continua. La segunda iteración se consigue dividiendo cada uno de esos cuatro cuadrados en otros cuatro y uniendo sus centros del mismo modo que en el caso anterior.
Otra curva “original” es la que creó el matemático Helge von Koch en 1904: “copo de nieve”. Partimos de un triángulo equilátero de lado unidad. Dividimos cada lado en tres partes iguales. Sustituimos el segmento central de cada lado por dos segmentos de tamaño idéntico al lado sustituido para formar un nuevo triángulo equilátero pero sin la “base”. Repetimos este proceso infinitas y lo que obtendremos es una línea de longitud infinita que encierra un área finita.
Esta curva fue una de las primeras que ha construido, con papiroflexia modular, mi alumnado con dificultades de aprendizaje.
Hoy en día este tipo de curvas se incluyen dentro de un tipo de objetos/monstruos matemáticos llamados fractales. Objetos que se obtienen mediante un proceso geométrico iterativo infinito. Podemos encontrar fractales en la distribución de galaxias, en procesos de ramificación, en fenómenos económicos, etc.
También podemos construir fractales en 3 dimensiones utilizando módulos Sonobé como:
La curva de Hilbert con 511 módulos.Esponjas de Menger niveles 1, 2 y 3. Se utilizaron 72, 1.056 y 18.000 módulos, respectivamente. Esta última construida por un grupo de 80 estudiantes durante 2 meses y acabada en febrero de 2007.Dentro del aula de matemáticas presentar al alumnado los procesos iterativos infinitos a través de la papiroflexia facilita la visualización de los mismos y aporta un enfoque más atractivo de la materia.
Papiroflexia recreativa: puzles, juegos…
El juego es una forma estimulante para aprender contenidos matemáticos en donde se trabaja, entre otros, la visualización espacial y la perseverancia a la hora de resolver un problema.
CUBO SOMA
El cubo Soma es un puzle creado en 1936 por Piet Hein. Para construirlo se van a necesitar 122 módulos Sonobé.
A la hora de ensamblar tantos módulos el alumnado mejorará su destreza manual fina para que el puzle quede lo más estético posible. Con estas 7 piezas se pueden resolver retos como construir figuras, letras (como la F del dibujo) e incluso números.Una actividad creativa que propongo al alumnado es obtener la letra π y sus cifras decimales (para la foto hemos utilizado 4 cubos Somas, uno para cada elemento):
Geometría ajedrecística
Hemos construido las 6 piezas de un juego de ajedrez con papiroflexia modular uniendo módulos cuadrados (en la parte superior de la torre aparece medio cuadrado) y módulos de triángulo equilátero. Con estas piezas podemos trabajar aspectos geométricos como:
- Indica en qué figura(s) aparecen los siguientes ángulos de: 45º, 60º, 90º, 120º, 180º, 105º = 60º + 45º, 150º = 90º + 60º…
- Comprueba en el peón la fórmula de Euler:caras + vértices = aristas + 2
- Calcula el área del hexágono que hay en la base del caballo.
- Escribe los nombres de los poliedros regulares. Localiza y nombra todos los poliedros que aparecen en las 6 figuras de ajedrez.
Sugerencias de papiroflexia modular matemática
Si queremos estimular la creatividad con la papiroflexia modular podemos combinarla con la electricidad y convertirse en Makers con proyectos como:Logotipo Maker Faire (con bipirámides)Lámpara (de cubo truncado)GAFAS LED (con módulo tortuga) El profesorado, desde su asignatura, puede establecer una red de vinculaciones educativas todo lo extensa que considere oportuno. Cada uno de estos “nudos” de la red también tiene sus propias vinculaciones dotando a todo el conjunto de una estructura fractal relacional.Si como docentes somos capaces de establecer los máximos “puentes” entre las diferentes partes implicadas, estamos facilitando la integración del alumnado en la sociedad adulta mediante una diversificación y graduación de objetivos factibles e individualizados y adecuando los criterios de evaluación a esta heterogeneidad en el aula para que el alumnado no se sienta excluido de este proceso de enseñanza-aprendizaje.Si el docente amplía su mirada, con la intención de detectar las fortalezas de su alumnado y ponerlas al servicio del grupo-clase para enriquecerlo y cohesionarlo, conseguirá favorecer el desarrollo de habilidades sociales en su alumnado creando un ambiente de aprendizaje significativo y muy estimulante. RM
